جایگشت ریاضی دهم یعنی هنر چیدن عناصر در حالتهای مختلف، اما برای بسیاری از دانشآموزان، این موضوع در نگاه اول سخت و گیجکننده بهنظر میرسد و برای همین در این مقاله سریعترین و سادهترین راه یادگیری، تحلیل، و جلوگیری از اشتباهات رایج را توضیح میدهیم.
وقتی دانشآموز میخواهد وارد دنیای جایگشت شود، معمولا اولین چیزی که در ذهنش شکل میگیرد، فرمولها و اعداد پیچیده است. اما واقعیت این است که اگر جایگشت از پایه و با تکنیک صحیح آموزش داده شود، نهتنها آسان است بلکه تبدیل به یکی از لذتبخشترین بخشهای ریاضی میشود. هدف این مقاله از دبیرستان اندیشه پارسیان که به عنوان بهترین دبیرستان دخترانه تهران شناخته میشود این است که کمک کند پایه دهمیها جایگشت را بدون حفظ کردن و فقط با «فهم واقعی» یاد بگیرند.
چرا یادگیری جایگشت برای پایه دهم دشوار میشود؟
بخشی از سختی یادگیری جایگشت ریاضی دهم ناشی از این است که ذهن بسیاری از دانشآموزان هنوز بین مفهوم «چیدن» و «انتخاب» تفاوت قائل نمیشود. جایگشت به نظم اهمیت میدهد، اما مغز انسان معمولا بهصورت شهودی نظم را در انتخابهایش لحاظ نمیکند. وقتی دانشآموز چند عنصر را برمیدارد، ناخودآگاه تصور میکند هر انتخاب فقط یک حالت دارد، در حالی که جایگشت ثبت میکند هر تغییر مکان کوچک یک حالت جدید است. این عدم درک، منجر به اشتباهات بزرگ در تحلیل مسائل میشود.
از طرفی، برخورد اولیه دانشآموز با فرمول n! یا فرمولهای شرطدار باعث میشود فکر کند جایگشت یک بخش خشک و فرمولمحور از ریاضی است. در حالی که اگر به او گفته شود جایگشت فقط یک روش شمارش منظم است، ذهنش باز میشود و یادگیری بسیار سادهتر خواهد بود.
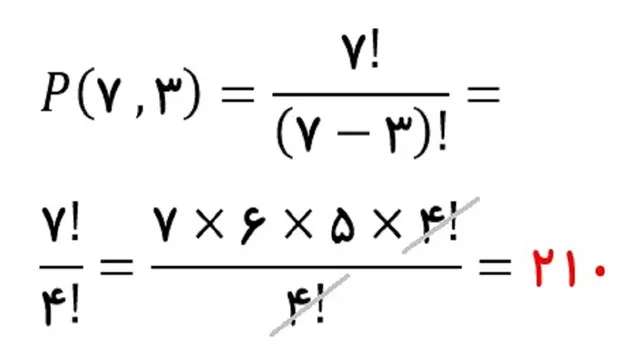
درک واقعی مفهوم جایگشت ریاضی دهم بدون حفظ فرمول
برای اینکه جایگشت ریاضی دهم در ذهن ماندگار شود، باید دانشآموز بفهمد که جایگشت در زندگی روزمره فراوان است: ترتیب ورود افراد به کلاس، شمارهگذاری صندلیها، یا حتی ترتیب پوشیدن لباسها. وقتی دانشآموز متوجه میشود جایگشت یک رفتار طبیعی ذهن است، دیگر فرمولها برایش سنگین به نظر نمیرسند.
اگر دانشآموز بتواند معنای n! را بهعنوان تعداد روشهای «چیدن» درک کند، در حل مسائل پیچیده نیز دچار سردرگمی نمیشود. بنابراین بهجای حفظکردن، باید تصویرسازی ذهنی انجام شود؛ یعنی باید بتواند تصور کند عناصر چگونه در جایگاهها قرار میگیرند و چه تعداد جایگاه خالی باقی مانده است.
تکنیک تصویرسازی و چیدمان مرحلهای برای حل مسائل
یکی از مهمترین مهارتهایی که یادگیری جایگشت ریاضی دهم را سریع میکند، تصویرسازی است. اگر دانشآموز بتواند مسئله را روی کاغذ به شکل جایگاههای خالی رسم کند، بخش بزرگی از سختی موضوع برطرف میشود. نحوه پر شدن این جایگاهها، ذهن او را هدایت میکند تا بفهمد در هر مرحله چند انتخاب آزاد دارد.
این روش بهویژه در مسائل شرطدار بسیار راهگشا است، چون برای مثال وقتی گفته میشود دو نفر نباید کنار هم بنشینند، تصویر جایگاهها کمک میکند این شرط را به وضوح ببینیم. دیدن مسئله، همیشه آن را سادهتر از شنیدن یا حفظ کردن میکند.
چگونه مسائل شرطدار جایگشت را بدون خطا تحلیل کنیم؟
مسائل شرطدار همیشه چالشبرانگیزند و بیشترین اشتباهات در امتحانها مربوط به همین بخش از جایگشت ریاضی دهم است. ابتدا باید شرط را به زبان ساده ترجمه کرد. مثلا اگر گفته شود دو نفر کنار هم نباشند، بهجای تلاش برای حذف کردن تکتک حالات، بهتر است ابتدا کل حالات ممکن را محاسبه کنیم و سپس حالاتی را که در آنها شرط نقض میشود از کل کم کنیم.
این روش که به «اصل متمم» معروف است، تحلیل ذهنی را آسانتر میکند. در نتیجه، دانشآموز به جای مقابله با مسئله، با آن همکاری میکند؛ چون مسئله واضحتر و قابلکنترلتر میشود.

نقش درخت حالات در کاهش اشتباهات دانشآموز
درخت حالات زمانی که مسئله پیچیده است بسیار کمککننده است. مثلا در مسالهای که باید انتخاب کنیم «اگر اولین جایگاه توسط A پر شود، دومین جایگاه چند انتخاب دارد؟» درخت حالات یک نمودار بصری است که جریان تصمیمگیری را مرحله به مرحله نمایش میدهد. وقتی دانشآموز مسیرهای مختلف را مقابل خود میبیند، احتمال اینکه بخشی از حالات را فراموش کند بسیار کمتر میشود.
بههمین دلیل، بسیاری از معلمان توصیه میکنند برای یادگیری جایگشت ریاضی دهم ابتدا یکی دو مسئله را با درخت حالات حل کنید تا ذهنتان با ساختار مسائل آشنا شود.
جایگشت با عناصر تکراری؛ چگونه از اشتباهات پرتکرار جلوگیری کنیم؟
بخشی از مشکلات آموزشی جایگشت ریاضی دهم مربوط به وجود عناصر تکراری است. مثلا در یک کلمه مانند صف، دانشآموز ممکن است گمان کند تعداد جایگشتها برابر ۵! است، اما واقعیت این است که وجود حروف تکراری باعث میشود تعداد حالات واقعی کمتر شود. برای همین است که فرمول جایگشت با عناصر تکراری به شکل n! / (n1! n2! n3!) تعریف میشود.
اما فهم این فرمول نیازمند توضیح مفهومی است: اگر دو حرف یکسان داریم، هر بار که جای آنها را عوض کنیم، ظاهر چیدمان تغییری نمیکند؛ بنابراین حالت جدیدی ایجاد نشده است. فهمیدن همین نکته باعث میشود ذهن دانشآموز از پیچیدگی بیدلیل آزاد شود.
تفاوت ترکیب و جایگشت: کلید حل صحیح تستها
یکی از نقاط حساس جایگشت ریاضی دهم تشخیص تفاوت آن با ترکیب است. ترکیب فقط انتخاب میکند، اما جایگشت انتخاب و ترتیب میدهد. این تفاوت زمانی مهم است که در تستها عباراتی مانند «چند نفر را انتخاب کنید» یا «چند نفر را بچینید» میآید. اگر دانشآموز این تفاوت را بهخوبی درک نکند، ممکن است همیشه از فرمول اشتباه استفاده کند. بهترین تمرین این است که از خود بپرسید: «آیا ترتیب اهمیت دارد؟» اگر جواب مثبت بود، جایگشت است و اگر نه، ترکیب. درک همین سوال ساده، نیمی از مسائل را حل میکند.
روشهای افزایش سرعت حل تستهای جایگشتی در امتحانات
سرعت در حل مسائل جایگشت ریاضی دهم با تمرین حاصل میشود، اما تمرین باید هوشمندانه باشد. دانشآموز باید ابتدا روی مسائل سادهتر که ساختار پایهای دارند کار کند و بعد سراغ مسائل شرطدار برود. سرعت زمانی افزایش پیدا میکند که ذهن به فرمولها و سطح انتخابها عادت کند. همچنین مرور مداوم مسئلهها، استفاده از تکنیکهای تصویرسازی و حل تستهای واقعی سالهای قبل باعث میشود ذهن مسیرهای حل را سریعتر تشخیص دهد.

مقایسه رویکردهای آموزشی در یادگیری جایگشت
| رویکرد آموزشی | ویژگی | نتیجه برای دانشآموز |
| آموزش فرمولمحور | تکیه بر حفظ روابط | احتمال اشتباه بالا |
| آموزش شهودی | استفاده از تصویرسازی و جایگاهها | فهم عمیق و ماندگار |
| آموزش مسئلهمحور | تمرین با مثالهای واقعی | افزایش سرعت حل تست |
| آموزش ترکیبی | تلفیق شهود، فرمول و تکنیکها | بهترین عملکرد تحصیلی |
طبق گزارش رسمی TIMSS ، کشورهایی که برنامه درسی آنها بر «درک مفهومی» تأکید دارد، میانگین نمرات ریاضی دانشآموزان آنها ۱۲ تا ۱۸ درصد بالاتر از کشورهایی است که تمرکز را صرفا روی حفظکردن فرمولها میگذارند. این آمار نشان میدهد در یادگیری موضوعاتی مثل جایگشت ریاضی دهم، موفقیت زمانی حاصل میشود که دانشآموز مفهوم را لمس کند، نه اینکه صرفا روابط را حفظ کند.
جمعبندی
در نهایت، یادگیری جایگشت ریاضی دهم فقط با یک رویکرد درست میتواند برای دانشآموز آسان، لذتبخش و کاملا قابلفهم شود. وقتی جایگشت از سطح فرمول فراتر میرود و تبدیل به تصویرسازی و درک واقعیِ «چیدن» میشود، ذهن دانشآموز به همان سمتی حرکت میکند که ریاضی از او میخواهد.
اگر بهدنبال محیطی هستید که فرزند شما بتواند چنین آموزش مفهومی و اصولی را تجربه کند، انتخاب یک مدرسه با کیفیت بالا مانند اندیشه پارسیان اهمیت زیادی پیدا میکند، جایی که بهترین دبیرستان دخترانه تهران با روش آموزشی نوین و مبتنی بر درک مفهومی، مسیر یادگیری ریاضی را برای دانشآموزان هموار کرده است.

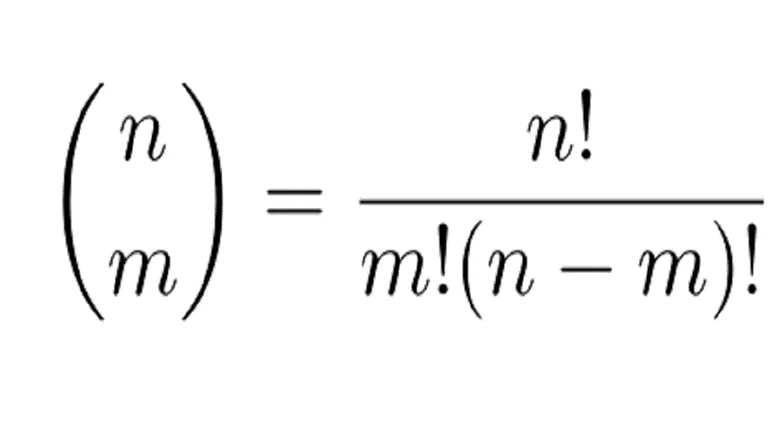

من همیشه با مبحث جایگشت مشکل داشتم، مخصوصا وقتی تعداد حالتها زیاد میشه قاطی میکنم. توضیحاتی که اینجا دادین خیلی ساده و روشن بود. فهمیدم چطور باید تعداد ترتیبهای مختلف رو حساب کنم. برای دانشآموزای دهمی خیلی میتونه کمککننده باشه. ممنون