تابع ریاضی دهم یکی از مفاهیمی است که اگر خوب درک شود، پایه بسیاری از مباحث پیشرفتهتر مثل مثلثات، نمودارها و معادلات خطی و غیرخطی خواهد بود؛ تابع در واقع یک قانون یا رابطه مشخص است که به هر ورودی (عدد یا مقدار) دقیقا یک خروجی اختصاص میدهد و این یعنی کارکرد تابع پیشبینیپذیر و دقیق است. به این ترتیب وقتی ورودی را بدانیم، خروجی را هم بهصورت قطعی خواهیم داشت. این ویژگی باعث میشود تابع ابزاری بسیار قدرتمند برای مدلسازی روابط بین کمیتها باشد.
اگر مدرسهای بخواهد این مفهوم را اصولی و مفهومی آموزش دهد، شبیه کاری است که در بهترین دبیرستان دخترانه غرب تهران یعنی اندیشه پارسیان انجام میشود؛ آنها تابع را صرفا بهعنوان یک مبحث حفظی قرار نمیدهند، بلکه به دانشآموز یاد میدهند که چگونه رابطهها و الگوهای دنیای واقعی را با تابع ببینند و تحلیل کنند.
تابع دقیقا چه چیزی را مدلسازی میکند؟ فهم تابع با مثالهای واقعی دنیای اطراف
برای درک واقعی تابع باید ابتدا بفهمیم یک تابع چه کاری انجام میدهد. تابع چیزی جز «رابطه ورودی → خروجی» نیست. این رابطه میتواند ساده یا پیچیده باشد، خطی یا غیرخطی، ولی اصل آن ثابت است: هر ورودی، دقیقا یک خروجی معین. تصور کن ماشینی باشد که «عدد اول» را واردش میکنی مثلا ۵ و ماشین طبق قانون داخلش، مثلا «ضرب در ۲ و بعلاوه ۳» عمل میکند، و خروجی آن ۱۳ است. اگر ورودی ۷ باشد، خروجی ۱۷؛ اگر ورودی ۰ باشد، خروجی ۳. این ماشین یک تابع است.
در دنیای واقعی مثالهای فراوان وجود دارد: قیمت نهایی کالا تابعی از قیمت پایه و مالیات است؛ ارتفاع آبی که یک تانک پس از پر شدن تابعی از زمان پر شدن است؛ سرعت متوسط یک دوچرخهسوار تابعی از مسافت طی شده و زمان است. وقتی رابطه ورودی و خروجی مشخص باشد، تابع امکان پیشبینی ایجاد میکند.
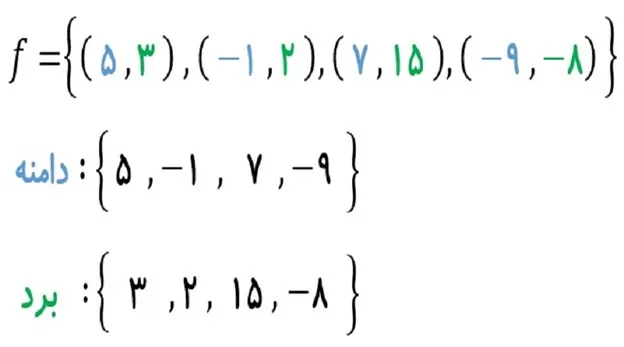
در دروس مدرسه، وقتی به مبحث تابع در پایه دهم میرسیم، معلم ممکن است تابع را بهصورت فرمولی مثل f(x)=2x+3 معرفی کند؛ اما شاید مهمتر این باشد که دانشآموز بداند این فرمول دقیقا چه چیزی مدل میکند: رابطه بین یک متغیر «x» و یک متغیر «y» (خروجی). اگر x تغییر کند، y نیز طبق همان قانون تغییر میکند. این همان قدرت تابع است، مدلسازی روابط بین مقادیر، پیشبینی خروجی و تحلیل نتایج.
تابع ریاضی دهم با این نگاه نه یک درس خشک بلکه یک ابزار برای دیدن «چگونگی ارتباط کمیتها» است. وقتی این ابزار را درست بفهمیم، میتوانیم از آن برای تحلیل مسائل واقعی استفاده کنیم: مثلا اگر بدانیم هزینه برق تابعی از مصرف است، میتوانیم هزینه ۱۰ ماه آینده را برآورد کنیم؛ یا اگر بدانیم مسافت طیشده تابعی از زمان است، سرعت لازم برای رسیدن به مقصد را محاسبه کنیم. در نتیجه تابع چیزی نیست که فقط سر جلسه امتحان کاربرد داشته باشد؛ یک مهارت تحلیلی برای زندگی است.
دامنه تابع؛ از اشتباهات رایج تا روش تشخیص سریع و قطعی
دامنه تابع یعنی مجموعه تمام مقادیری از ورودی که تابع برای آنها تعریف شده است. وقتی میگوییم «دامنه تابع»، منظورمان این است که تابع برای همه عددها اجرا نمیشود؛ گاهی برخی عددها را نمیپذیرد. مثلا تابعی به شکل f(x)= را در نظر بگیر: این تابع برای x=0 تعریف نمیشود، چون تقسیم بر صفر بیمعناست. بنابراین دامنه این تابع همه اعداد حقیقی بهجز صفر است.
بسیاری از دانشآموزان و حتی بعضی معلمان در تشخیص دامنه اشتباه میکنند. اشتباه رایج این است که دامنه را بهصورت فرضی «همه اعداد» در نظر میگیرند، بدون اینکه صورت تابع را تحلیل کنند. برای تشخیص دامنه صحیح باید قوانین زیر رعایت شود: اول ببینید آیا صورت تابع شامل کسری هست؟ اگر هست، مخرج نباید صفر شود. دوم اگر ریشه (جذر) دارید، داخل ریشه نباید منفی شود مگر اینکه تابع مختص به اعداد مختلط باشد. سوم اگر لگاریتم یا تابع خاص دارد، شرط تعریف آن رعایت شود (مثلا داخل لگاریتم باید مثبت باشد). یعنی دامنه تابع دقیقا مجموعه اعداد حقیقیای است که تابع برای آنها تعریف شده و خروجی واقعی میدهد.
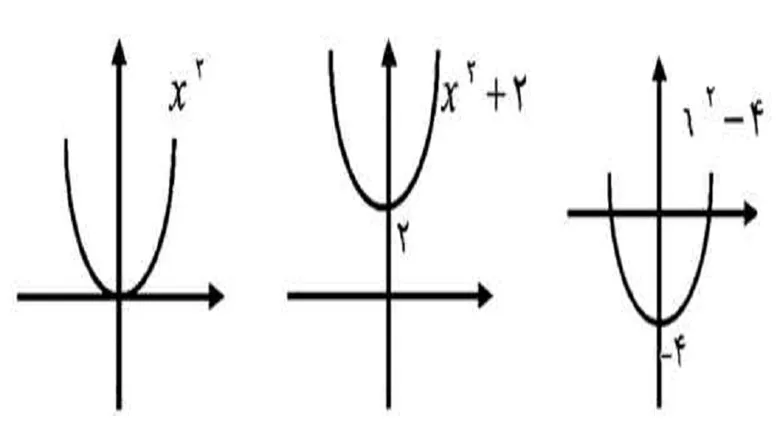
برد تابع؛ چگونه بفهمیم خروجیها دقیقا کدام عددها هستند؟ (نسخه آموزشی پایه دهم)
بعد از دامنه، قدم بعدی در درک تابع، برد آن است. برد تابع یعنی مجموعه تمام خروجیهایی که تابع از دامنه خود تولید میکند. اگر دامنه را بهعنوان تمام ورودیهای مجاز ببینیم، برد مجموعه خروجیهای ممکن است. در درس تابع ریاضی دهم معمولا تمرکز بر تشخیص دامنه است، اما برد همانقدر مهم است چون نشان میدهد تابع چه مقادیری از خروجی میتواند بدهد. مثلا آیا همیشه مثبت است؟ آیا میتواند منفی شود؟ آیا همه اعداد حقیقی را میپذیرد یا محدود است؟
برای پیدا کردن برد تابع، ابتدا باید ببینیم تابع چگونه ورودی را به خروجی تبدیل میکند. سادهترین روش برای توابع خطی مثل f(x)=2x+3 این است که دامنه تمام اعداد حقیقی است و چون ضریب x مثبت است، خروجی هم تمام اعداد حقیقی را پوشش میدهد، یعنی برد = ℝ. اما در توابع غیرخطی، مثلاً f(x)=x2f(x) = x^2f(x)=x2، دامنه ℝ است اما برد تابع فقط اعداد ≥ ۰ است، چون مربع یک عدد هیچگاه منفی
رابطه میان نمودار تابع و دامنه و برد؛ خواندن شکل مثل یک زبان
نمودار تابع تصویری از رابطه عددی ورودی و خروجی است. وقتی نمودار تابع را نگاه میکنیم، در واقع داریم به یک زبان بصری گوش میدهیم؛ زبانی که با «محور افقی» برای دامنه ورودی x و «محور عمودی» برای برد خروجی y نمایان میشود. این زبان به ما کمک میکند تغییرات تابع، روند، حداقل و بیشینه و نقاط خاص را در یک نگاه ببینیم.
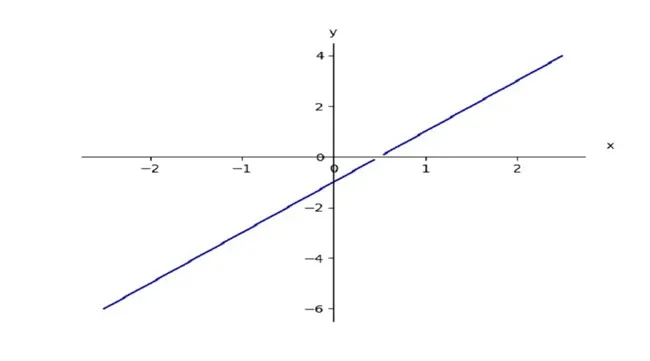
برای مثال، اگر نمودار تابعی را ببینیم که از چپ و راست باز بالا میرود و هیچ حد پایین ندارد، فورا میفهمیم دامنه احتمالا ℝ است و برد تابع نیز «همه اعداد بزرگتر از یک مقدار» است. اگر نمودار فقط برای x ≥ 0 تعریف شده باشد، یعنی دامنه تابع محدود است و بر نمودار این محدودیت با شکستی یا پایان در سمت چپ نمایش داده میشود. اگر نمودار تابع دارای قله یا دره باشد، یعنی تابع بیشینه یا کمینه دارد؛ این موضوع در تعیین برد بسیار مهم است.
در واقع یادگیری اینکه چگونه نمودار تابع را بخوانیم و از آن دامنه و برد را استخراج کنیم، شاهکلید تسلط روی مباحث تابع است. این مهارت باعث میشود دانشآموز بتواند بدون فرمول حتی با نمودار کار کند؛ یعنی اگر فقط شکل رسم شده باشد، بتواند سوال «دامنه چیست؟ برد چیست؟» را پاسخ دهد. این همان چیزی است که تابع را به «زبان ریاضی دیداری» تبدیل میکند. زبانی که بسیاری از دانشآموزان در درس تابع ریاضی دهم از آن غافل میشوند.
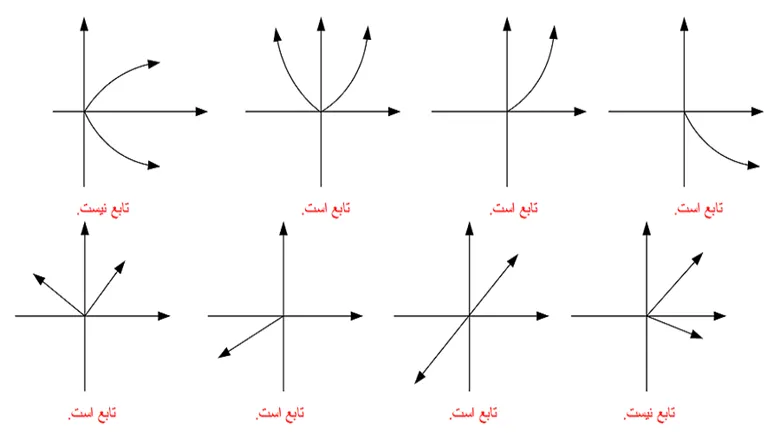
تابع با دامنه و برد متفاوت
| نوع تابع / ویژگی | دامنه | برد | نکته کلیدی |
| f(x)=2x+3 | ℝ | ℝ | تابع خطی؛ دامنه و برد آزاد |
| f(x)= | ℝ | y≥0 | خروجی همیشه غیرمنفی |
| f(x)= | ℝ \ {0} | ℝ \ {0} | مخرج صفر نیست ، ورودی ۰ منع شده |
| f(x)= | x≥1 | y≥0 | زیر ریشه باید غیرمنفی باشد |
جمعبندی
در نهایت، تابع ریاضی دهم نه تنها یک مبحث تحصیلی بلکه یک ابزار تحلیلی برای درک روابط بین کمیتهاست. زمانی فهم تابع کامل و کاربردی میشود که بتوانیم ورودی و خروجی را تشخیص دهیم، دامنه و برد را بهدرستی تعیین کنیم و نمودار را مثل یک زبان دوم بخوانیم. این توانایی فقط با یادگیری مفهومی نه حفظی ممکن است. اگر بخواهی در مسیر یادگیری عمیق تابع حرکت کنی، مهم است که نگاهت به تابع فقط بهعنوان یک فرمول محدود نباشد.
همچنین وقتی میخواهی آموزشی حرفهای و جدی بگیری، محیط و متد معلم اهمیت دارد. اندیشه پارسیان به عنوان بهترین دبیرستان دخترانه غرب تهران با رویکرد مفهومی و تحلیلی، دانشآموز را برای عملکرد پایدار در مباحث پیشرفته آماده میکند. تابع ریاضی دهم اگر بهدرستی یاد گرفته شود، پایه و بنای موفقیت در بسیاری از مباحث مهم ریاضی خواهد بود.


بدون دیدگاه