اتحاد و تجزیه پایه نهم در واقع زبان فشردهی ریاضی برای سادهسازی عبارتها و حل سریعتر معادلات است؛ اگر دانشآموز بداند هر اتحاد دقیقا چه الگویی را پنهان کرده و چطور آن را تشخیص دهد، بخش بزرگی از ترس ریاضی برای همیشه از بین میرود. در این مقاله قرار است یاد بگیریم اتحادها چه هستند، چرا فراموش میشوند و با چه روشی میتوان آنها را طوری یاد گرفت که واقعا یادت نره.
بسیاری از دانشآموزان پایه نهم تصور میکنند مشکل اصلی این فصل، حفظ کردن فرمولهاست؛ اما واقعیت این است که دشواری اتحاد و تجزیه پایه نهم بیشتر به «درک نکردن الگو» برمیگردد تا حفظ نکردن. وقتی دانشآموز فقط فرمول را میبیند اما منطق پشت آن را نمیفهمد، ذهنش آن را مثل یک اطلاعات موقت ذخیره میکند؛ درست همان چیزی که شب امتحان هست و روز بعد محو میشود. اتحادها در اصل توصیفهای ریاضی از رفتار عددها هستند و اگر این رفتار دیده نشود، فرمولها بیمعنا به نظر میرسند.
اتحادها دقیقا چه چیزی را توصیف میکنند؟
اتحادها نتیجهی طبیعی ضرب، توان و توزیع هستند. وقتی میگوییم مربع یک مجموع، در واقع داریم توضیح میدهیم که اگر دو عدد کنار هم قرار بگیرند و کل آنها به توان دو برسد، چه اتفاقی برای هر جزء میافتد. در اتحاد و تجزیه پایه نهم مهمترین نکته این است که دانشآموز بفهمد اتحادها فرمولهای جادویی نیستند؛ بلکه خلاصهشدهی محاسبات طولانیاند. هر اتحاد را میتوان با باز کردن پرانتزها و ضرب ساده دوباره ساخت، و همین قابلیت بازسازی است که یادگیری را ماندگار میکند.
روش «یادتنره!» یعنی یادگیری بر اساس تصویر ذهنی، الگو و کاربرد. مغز انسان اطلاعاتی را نگه میدارد که یا قابل تصور باشند، یا بارها در موقعیتهای مختلف دیده شوند. وقتی اتحادها فقط به شکل نماد ریاضی دیده میشوند، ذهن ارتباطی با آنها برقرار نمیکند. اما اگر هر اتحاد با یک داستان عددی، یک شکل هندسی یا یک مثال واقعی همراه شود، مغز آن را بهعنوان دانشی مفید ذخیره میکند. این دقیقا همان روشی است که در آموزشهای مفهومی در مدارس موفق، از جمله در بهترین دبیرستان دخترانه غرب تهران مانند اندیشه پارسیان استفاده میشود.
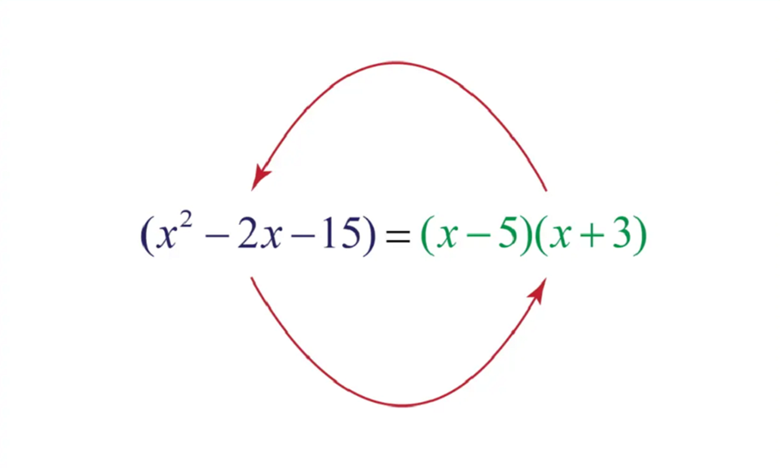
اتحاد مربع مجموع و مربع تفاضل؛ دو فرمول، یک منطق
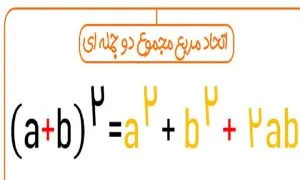
در نگاه اول، مربع مجموع و مربع تفاضل دو فرمول جداگانه به نظر میرسند، اما در واقع یک ساختار مشترک دارند. تفاوت فقط در علامت وسط است. اگر دانشآموز یاد بگیرد که «عدد اول مربع میشود، عدد دوم مربع میشود و دو برابر حاصلضربشان در وسط میآید»، دیگر نیازی به حفظ کردن کورکورانه ندارد. در اتحاد و تجزیه پایه نهم همین درک ساختاری باعث میشود دانشآموز بتواند هم اتحاد را بسط دهد و هم برعکس، تجزیه انجام دهد.
اتحاد مزدوج؛ چرا حذف وسط اتفاق میافتد؟
یکی از نقاط گیجکننده برای دانشآموزان این است که چرا در اتحاد مزدوج، جملهی وسط ناپدید میشود. پاسخ ساده است: چون دو جملهی وسط دقیقا همدیگر را خنثی میکنند. وقتی یک مجموع در یک تفاضل ضرب میشود، حاصلضربهای مثبت و منفی برابر ایجاد میشوند و جمعشان صفر میشود. این اتفاق تصادفی نیست، بلکه یک الگوی ثابت است. فهم این موضوع باعث میشود اتحاد مزدوج به یکی از سادهترین بخشهای اتحاد و تجزیه پایه نهم تبدیل شود، نه ترسناکترین.
تجزیه؛ حرکت معکوس اما هوشمندانه
اگر اتحاد بسط دادن باشد، تجزیه جمع کردن تکههاست. دانشآموزانی که تجزیه را سخت میدانند، معمولا اتحادها را بهدرستی نشناختهاند. تجزیه یعنی تشخیص اینکه این عبارت، حاصل کدام اتحاد است. در اتحاد و تجزیه پایه نهم، موفقیت در تجزیه دقیقا به توانایی دیدن الگوها بستگی دارد، نه سرعت محاسبه. هرچه الگوها بیشتر تمرین شوند، ذهن سریعتر آنها را تشخیص میدهد.
اشتباهات رایج دانشآموزان در اتحاد و تجزیه
بخش اتحاد و تجزیه پایه نهم یکی از مهمترین و در عین حال پرتلهترین فصلهای ریاضی است. بسیاری از دانشآموزان فرمولها را حفظ میکنند اما چون درک مفهومی ندارند، در حل سوالات ساده هم دچار خطا میشوند. این اشتباهات معمولا تکرارشوندهاند و اگر ریشهای اصلاح نشوند، در پایه دهم و یازدهم هم ادامه پیدا میکنند.
اشتباه اول: تشخیص اشتباه نوع اتحاد
یکی از رایجترین خطاها این است که دانشآموز فرمول اشتباه را برای عبارت انتخاب میکند. مثلا نمیداند با اتحاد مربع مجموع طرف است یا مربع تفاضل، یا اصلا اتحاد نیست و باید تجزیه انجام شود.
اشتباه دوم: فراموش کردن جملهی وسط در اتحادهای مربع
در اتحادهای مربع، جملهی وسط (±) بیشترین قربانی است!
خیلیها فکر میکنند مربع یعنی فقط مربع اول و دوم.
اشتباه سوم: اشتباه گرفتن اتحاد مزدوج با مربع تفاضل
اشتباه چهارم: تشخیص ندادن اینکه عبارت «قابل تجزیه» است
اگر همهی جملات یک عامل مشترک دارند، اولین قدم همیشه فاکتورگیری است.
اشتباه پنجم: عجله در محاسبه و بیدقتی در توانها
خیلی وقتها اشتباه دانشآموز نه از ندانستن، بلکه از عجله است.
توان روی متغیر هم اعمال میشود، نه فقط عدد.
تمرین زیاد بدون تحلیل، فایدهی چندانی ندارد. تمرین مؤثر یعنی بررسی اینکه چرا یک عبارت قابل تجزیه است و چرا دیگری نه. تحقیقات آموزشی نشان میدهد دانشآموزانی که تمرین تحلیلی دارند، تا ۴۰٪ عملکرد بهتری در مباحث جبری نشان میدهند.
مقایسه یادگیری حفظی و مفهومی در اتحادها
| روش یادگیری | میزان ماندگاری | خطای محاسباتی |
| حفظ فرمول | پایین | بالا |
| یادگیری مفهومی | بالا | بسیار کم |
طبق گزارش OECD – PISA 2022، دانشآموزانی که ریاضی را بهصورت مفهومی یاد میگیرند، بهطور میانگین ۳۲٪ عملکرد بهتر در حل مسائل ترکیبی دارند. این آمار نشان میدهد چرا در آموزشهای مدرن، از جمله در برنامههای آموزشی اتحاد و تجزیه پایه نهم، تمرکز از حفظ فرمول به درک ساختار تغییر کرده است.
دانشآموزی که این فصل را عمیق یاد بگیرد، در پایه دهم و یازدهم در مباحثی مثل معادلات درجه دوم، تابع و حتی حد و مشتق، مسیر بسیار هموارتری خواهد داشت. اتحاد و تجزیه پایه نهم پایهی بسیاری از مفاهیم آینده است و ضعف در آن مثل ساختن ساختمان روی زمین سست است.
جمعبندی نهایی
اگر بخواهیم صادقانه جمعبندی کنیم، مشکل اصلی دانشآموزان با اتحاد و تجزیه، سختی ذاتی این مبحث نیست، بلکه روش یادگیری اشتباه آن است. وقتی اتحادها بهصورت الگو، تصویر ذهنی و تحلیل آموزش داده شوند، نهتنها فراموش نمیشوند، بلکه به ابزار قدرتمند حل مسئله تبدیل میشوند. تجربهی مدارس موفقی مثل بهترین دبیرستان دخترانه غرب تهران یعنی اندیشه پارسیان نشان میدهد که آموزش مفهومی میتواند حتی سختترین فصل ریاضی را به یکی از شیرینترینها تبدیل کند.
بدون دیدگاه