مثلثات پایه یازدهم را ساده یاد بگیر: آموزش مفهومی، فرمول‌های مهم و راهکارهای حفظی

مثلثات پایه یازدهم یکی از مباحث کلیدی در ریاضیات متوسطه دوم است که درک درست آن نه تنها به موفقیت در امتحانات نهایی کمک می‌کند، بلکه پایه‌ای برای مباحث بعدی در ریاضیات، فیزیک و مهندسی فراهم می‌آورد. در این مقاله می‌خواهیم مثلثات پایه یازدهم را از پایه و با زبانی ساده، مفهومی و همراه با فرمول‌های کاربردی آموزش دهیم تا یادگیری آن برای هر دانش‌آموزی قابل‌فهم و لذت‌بخش شود.
یادگیری این مبحث نیاز دارد که مفاهیم زوایا، نسبت‌های مثلثاتی، اتحادها و کاربردهای مهم آن‌ها در مسائل واقعی به‌خوبی فهمیده شوند و سپس با تمرین‌های هدفمند تثبیت شوند.

در بسیاری از مدارس موفق از جمله مدرسه غیرانتفاعی دخترانه منطقه 22، آموزش مثلثات زمانی بیشترین بازده را دارد که دانش‌آموز ابتدا درک درستی از مفهوم نسبت‌های مثلثاتی پیدا کند و سپس فرمول‌ها را در قالب کاربردی تمرین کند. در مدارس اندیشه پارسیان نیز تاکید بر این است که دانش‌آموزان مثلثات را نه صرفا حفظی، بلکه با فهم عمیق و دید مسئله‌محور یاد بگیرند تا این مبحث به نقطه قوت آن‌ها در امتحانات تبدیل شود.

مثلثات پایه یازدهم چیست و چرا اهمیت دارد؟

مثلثات شاخه‌ای از ریاضیات است که به بررسی روابط بین زوایا و طول ضلع‌ها در مثلث‌ها می‌پردازد و نقش اساسی در حل مسائل هندسی، فیزیکی و مهندسی دارد. در مثلثات پایه یازدهم دانش‌آموزان با ابزارهایی آشنا می‌شوند که برای فهم صحیح این روابط ضروری هستند. این بخش شامل تعریف زاویه، اندازه‌گیری زاویه‌ها در درجه و رادیان، نسبت‌های مثلثاتی ابتدایی، و اتحادهای مهم مثل  sin، cos  و tan است. طبق منابع آموزش ریاضی پایه یازدهم، دایره مثلثاتی، تبدیل واحدها و محاسبه نسبت‌های مثلثاتی برای زوایای خاص از بخش‌های مهم این مبحثهستند که در برنامه درسی قرار گرفته‌اند.

اهمیت مثلثات پایه یازدهم از این جهت است که این مفاهیم نه تنها در امتحانات مدرسه (مثل امتحان نهایی) کاربرد دارند، بلکه در دروس بعدی مانند حسابان، فیزیک، و حتی در حل مسائل حرفه‌ای در مهندسی هم مورد استفاده قرار می‌گیرند. بسیاری از دانش‌آموزان هنگام مواجهه با این فصل به دلیل حجم زیاد فرمول‌ها دچار سردرگمی می‌شوند، اما اگر این مبحث را از دید مفهومی بفهمند، فرمول‌ها خود به‌خود قابل‌دسترس‌تر می‌شوند.

آشنایی مفهومی با 3 نسبت‌ مثلثاتی مهم

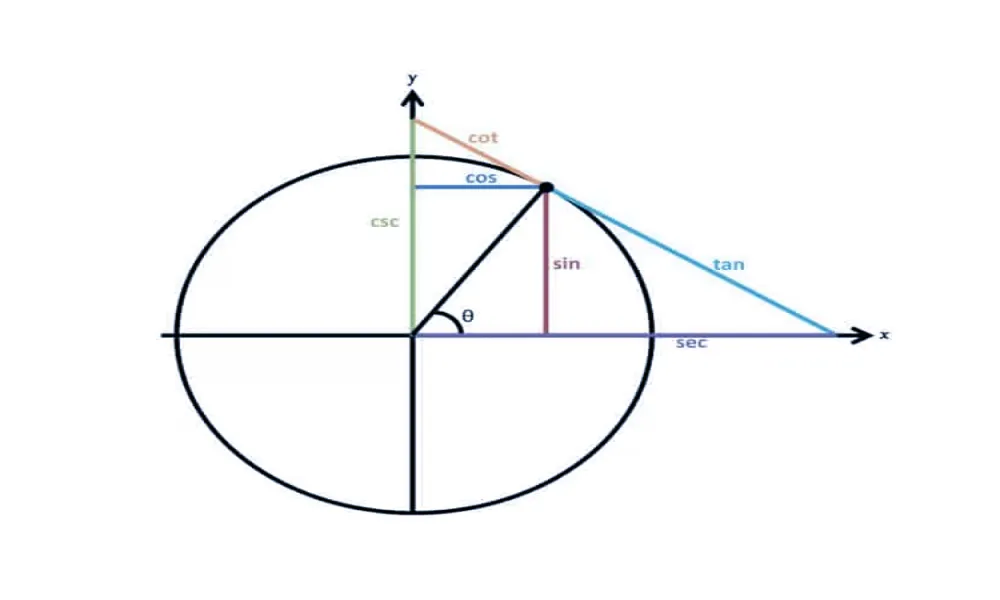
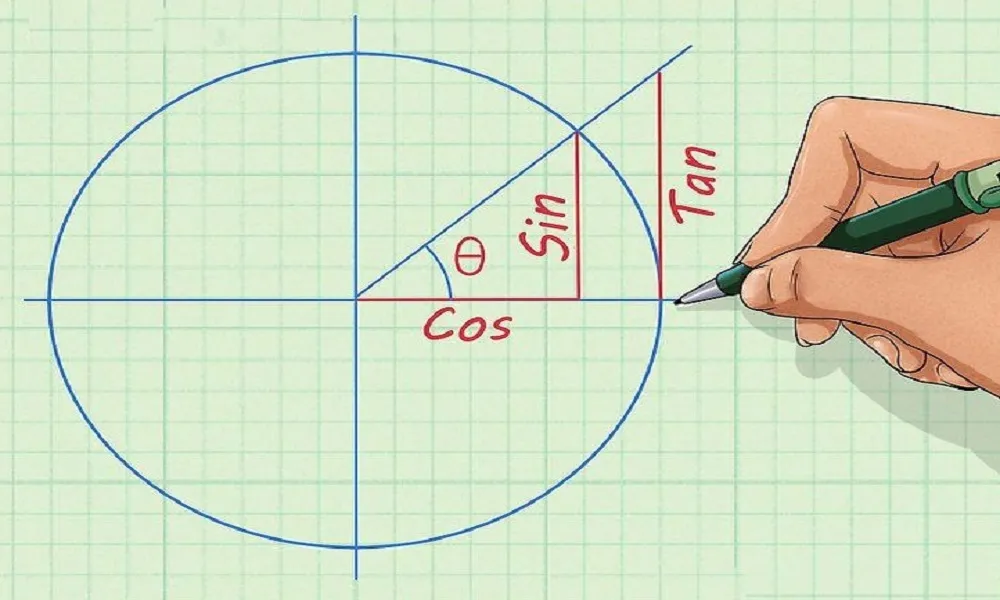
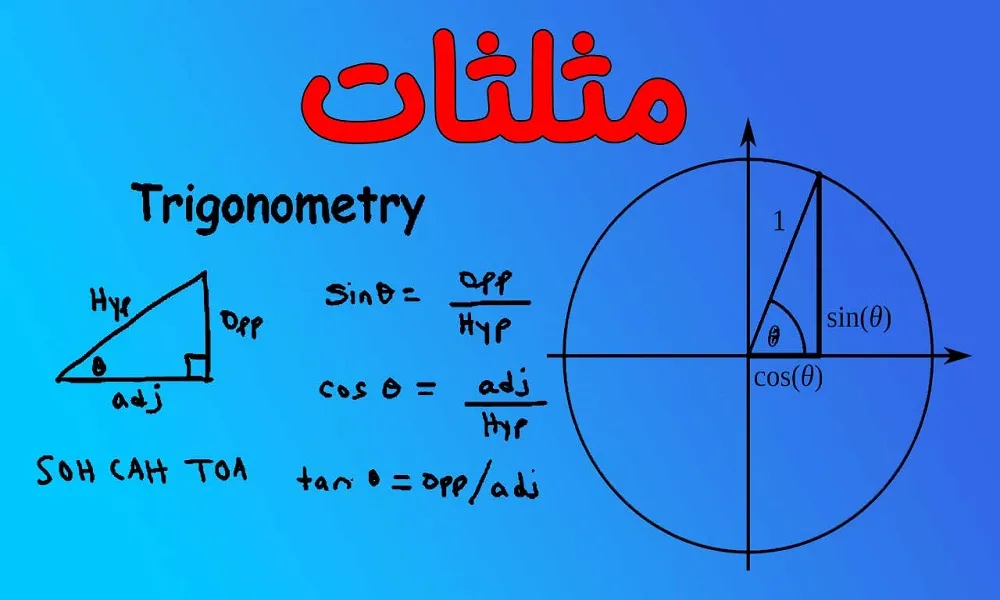
در مثلثات پایه یازدهم، اولین گام مهم یادگیری تعریف نسبت‌های مثلثاتی در مثلث قائم‌الزاویه است. این نسبت‌ها به‌عنوان ابزارهای بنیادی برای اندازه‌گیری زوایا و تحلیل رابطه اضلاع تعریف می‌شوند. سه نسبت اصلی عبارت‌اند از:

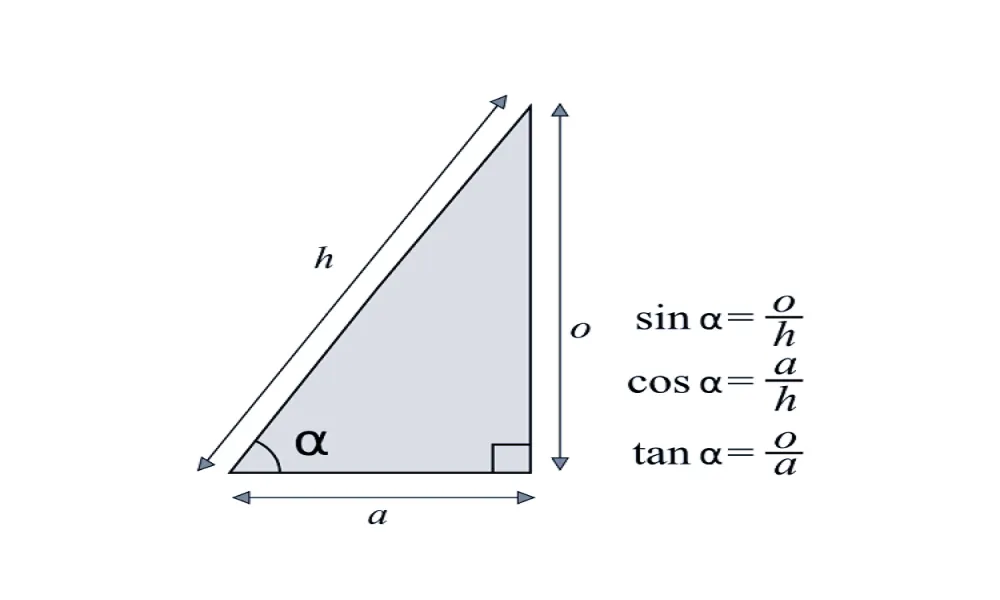
نسبت اول: سینوس(sin):  نسبت ضلع مقابل به وتر مثلث

نسبت دوم: کسینوس(cos):  نسبت ضلع مجاور به وتر مثلث

نسبت سوم: تانژانت(tan):  نسبت ضلع مقابل به ضلع مجاور

این تعریف‌ها زمانی روشن‌تر می‌شوند که یک مثلث قائم‌الزاویه را با زاویه θ در نظر بگیریم و نسبت هر ضلع را به وتر بررسی کنیم؛ این نسبت‌ها اساس تمام فرمول‌های مثلثات پایه یازدهم هستند و اگر درک درستی از آن‌ها پیدا کنید، مابقی مفاهیم بسیار ساده‌تر خواهند بود.

مثلا اگر نسبت سینوس θ را بدانیم، می‌توانیم به‌راحتی مقدار کسینوس آن زاویه را از اتحاد سینوس و کسینوس استخراج کنیم:
sin²θ + cos²θ = 1
که این اتحاد یکی از اصلی‌ترین روابط در مثلثات پایه یازدهم است.

فرمول‌های مهم مثلثات که باید بدانید

وقتی صحبت از فرمول‌های مهم در مثلثات پایه یازدهم می‌شود، مجموعه‌ای از روابط هستند که یادگیری آن‌ها کار حل سریع و صحیح مسائل را بسیار راحت‌تر می‌کند. این فرمول‌ها شامل اتحادهای مثلثاتی، تبدیل درجه به رادیان، و روابط ویژه برای زاویه‌های خاص هستند. برخی از مهم‌ترین فرمول‌ها به‌صورت زیرند:

الف. اتحادهای مثلثاتی پایه

sin²θ + cos²θ = 1

tanθ = sinθ / cosθ

این فرمول‌ها نه فقط بر اساس تعریف بلکه از طریق دایره مثلثاتی هم قابل‌اثبات هستند و بخش زیادی از پاسخ سوالات مثلثات پایه یازدهم را تشکیل می‌دهند.

ب. فرمول‌های زوایای خاص

برای زاویه‌های 30°، 45° و 60° مقدار نسبت‌های مثلثاتی ثابت است و باید آن‌ها را حفظ کرد چون در بسیاری از سوالات به‌کار می‌روند. برای مثال:

sin 30° = 1/2

cos 45° = √2/2

tan 60° = √3

یادگیری این فرمول‌های بنیادی که در مثلثات پایه یازدهم به‌صورت پیوسته تکرار می‌شوند به حل سریع سوالات کمک می‌کند.

نکات حفظی و تکنیک‌های یادگیری

در یادگیری مثلثات پایه یازدهم حفظ کردن فرمول‌ها بخش مهمی از فرآیند است، اما حفظ ساده بدون درک کاربردی منجر به فراموشی سریع می‌شود. برای حفظ بهتر فرمول‌ها، می‌توانید از تکنیک‌های زیر استفاده کنید:

• دسته‌بندی فرمول‌ها در قالب جدول یا نمودار
• ترسیم مثلث‌های مخصوص زاویه‌های ویژه
• تمرین با مثال‌های واقعی از طریق دایره مثلثاتی
• ساخت فلش‌کارت برای نسبت‌های مثلثاتی

با استفاده از این تکنیک‌ها نه‌فقط فرمول‌ها را حفظ می‌کنید، بلکه آن‌ها را در ذهن خود به‌عنوان ابزار حل مسئله می‌بینید و یادگیری در ذهن‌تان تثبیت می‌شود.

نکات مفهومی که طراحان سوال به آن‌ها علاقه دارند

در مثلثات پایه یازدهم اکثر طراحان سوال به مباحثی تمرکز می‌کنند که نشان دهنده درک مفهومی دانش‌آموز باشد. به همین دلیل باید به نکات زیر توجه ویژه داشته باشید:

1. ارتباط بین دایره مثلثاتی و نسبت‌های مثلثاتی
2. تبدیل زاویه‌ها از درجه به رادیان
3. چرایی اتحادهای مثلثاتی، نه فقط نحوه استفاده از آن‌ها
4. کاربرد نسبت‌های مثلثاتی در حل مسائل واقعی هندسی

این دیدگاه باعث می‌شود که وقتی با سؤال مواجه می‌شوید، بتوانید از پس آن نه فقط با حفظ کردن بلکه با درک عمیق نیز برآیید.

نقش دایره مثلثاتی در فهم عمیق مثلثات پایه یازدهم

یکی از نقاط عطف در یادگیری مفهومی مثلثات پایه یازدهم، درک صحیح دایره مثلثاتی است. بسیاری از دانش‌آموزان مثلثات را فقط محدود به مثلث قائم‌الزاویه می‌بینند، در حالی که دایره مثلثاتی ابزار اصلی برای گسترش این مفاهیم به تمام زوایا (بزرگ‌تر از ۹۰ درجه و حتی منفی) است. دایره مثلثاتی، دایره‌ای به شعاع یک واحد است که مرکز آن در مبدأ دستگاه مختصات قرار دارد و هر زاویه θ روی آن به یک نقطه مشخص با مختصات (cosθ , sinθ) متناظر می‌شود.

وقتی دانش‌آموز مفهوم دایره مثلثاتی را به‌درستی درک کند، بسیاری از فرمول‌ها و روابط مثلثات پایه یازدهم دیگر نیاز به حفظ کردن ندارند، بلکه به‌صورت منطقی قابل استخراج هستند. به عنوان مثال، دلیل اینکه مقدار سینوس و کسینوس هیچ‌گاه از ۱ بزرگ‌تر یا از ۱- کوچک‌تر نمی‌شود، دقیقا به شعاع واحد این دایره مربوط است. همچنین تغییر علامت سینوس و کسینوس در ربع‌های مختلف صفحه مختصات، تنها با نگاه کردن به جایگاه نقطه روی دایره مثلثاتی قابل تشخیص است.

دایره مثلثاتی کمک می‌کند تا دانش‌آموز بفهمد چرا در بعضی زوایا مقدار تانژانت تعریف‌نشده است یا چرا برخی اتحادهای مثلثاتی همیشه برقرار هستند. در مثلثات پایه یازدهم، بسیاری از سوال‌های مفهومی دقیقا بر پایه همین درک طراحی می‌شوند؛ یعنی طراح انتظار دارد دانش‌آموز بداند که نسبت‌های مثلثاتی فقط اعداد حفظی نیستند، بلکه بیانگر مختصات هندسی و روابط فضایی هستند. بنابراین تسلط بر دایره مثلثاتی نه‌تنها یادگیری این فصل را ساده‌تر می‌کند، بلکه پایه‌ای محکم برای مباحث پیشرفته‌تر ریاضی در سال‌های بعد می‌سازد.

اشتباهات رایج در مثلثات

یکی از بخش‌های مهم آموزش مثلثات پایه یازدهم آشنایی با اشتباهات متداول است که دانش‌آموزان اغلب به‌همین دلیل نمره از دست می‌دهند. برخی از رایج‌ترین این اشتباهات عبارت‌اند از:

1. اشتباه در تبدیل درجه به رادیان
2. استفاده نادرست از اتحادهای مثلثاتی
3. فراموش کردن علامت نسبت در ربع‌های مختصاتی
4. اشتباه در پاسخ سریع به سؤال‌های عددی بدون بررسی منطقی

اجتناب از این خطاها نیازمند تمرین مداوم و درک عمیق نسبت‌ها و فرمول‌هاست.

مروری بر مثلثات پایه یازدهم

بخش	تعریف	کاربرد
نسبت‌های مثلثاتی	سینوس، کسینوس، تانژانت	پایه برای حل سوالات زاویه و ضلع
اتحادهای مثلثاتی	sin²θ+cos²θ=1	ساده‌سازی محاسبات
زاویه‌های خاص	30°,45°,60°	تست‌های سریع و فرمول‌های کاربردی
دایره مثلثاتی	تبدیل زاویه به مختصات	درک بهتر توابع

تحقیقات آموزشی نشان داده‌اند که بسیاری از دانش‌آموزان پس از آموزش استاندارد مثلثات در کلاس موفق به درک مفاهیم نشده‌اند و عملکرد آن‌ها در آزمون‌های پس از درس پایین بوده است. در یک مطالعه رسمی در زمینه یادگیری توابع مثلثاتی در سطح دبیرستان، مشخص شد که دانش‌آموزان پس از تکمیل دوره مثلثات در کلاس نتوانسته‌اند تسلط مفهومی کافی بر روی نسبت‌های مثلثاتی و توابع مرتبط پیدا کنند؛ این مورد نشان می‌دهد نیاز به روش‌های آموزش مؤثرتر در مثلثات وجود دارد.

جمع‌بندی نهایی

در این آموزش جامع مثلثات پایه یازدهم را از دید مفهومی، فرمولی و کاربردی بررسی کردیم. فهم نسبت‌های مثلثاتی، اتحادهای مهم، یادگیری فرمول‌های کاربردی و اجتناب از اشتباهات رایج، از ارکان اصلی تسلط بر مثلثات هستند. به یاد داشته باشید که حفظ صورت‌مسئله‌ها به‌تنهایی کافی نیست؛ بلکه درک عمیق مفاهیم و به‌کارگیری آن‌ها در حل مسائل است که باعث می‌شود شما در مثلثات پایه یازدهم به یک تسلط واقعی برسید.